OCVは，on chip variationの略である。同じ形状や特性に設計された複数のトランジスタや配線は同一のチップに集積されたとしても，バラついてしまう。チップ全体にわたって，同じ素子が正確に均一に仕上がるわけではないからだ。同じ形状や特性に設計された素子が１チップ内でバラつく現象をOCVと呼ぶ。
一般に，OCVは次の三つの成分からなる。（1）各素子間で無秩序にばらつく「ランダム・バラつき」，（2）素子間の距離に依存して相関を持つ「距離依存バラらつき」（システマティック・バラつき），（3）チップ上の位置で決まったバラつきを持つ「デターミニスティック・バラつき」である。
タイミング設計にOCV考慮が必須
従来からチップ間の素子バラつきは考慮されてきたが，一つのチップ内の素子はすべて均一に仕上がるという前提の下で，タイミング設計が進められてきた。しかし半導体製造プロセスが微細になるにつれて，この前提が成り立たないケースが増えてきた。
特にトランジスタのランダム・バラつきは，プロセス世代が進むにつれて非常に大きくなってきている。先端のプロセス世代では，トタンジスタのOCVのランダム・バラつき成分は，チップ間のトランジスタ・バラつきと同じくらいの大きさになっている。このため，タイミング設計時にOCVを考慮することが必須となってきた。
以下では，上述したOCVの三つの成分を説明し，OCVをSTA（静的タイミング解析）に反映させる手法を紹介する。
ランダム・バラつき
各素子間でまったく無秩序にバラつくバラつきを，ランダム・バラつきと呼ぶ。一つのチップ内で隣り合う素子であっても，異なるチップの同じ位置にレイアウトされた素子であっても，無秩序にバラつく。
ランダム・バラつきの大きさは，素子の面積（たとえばトランジスタでは，ゲート長とゲート幅の積）の平方根に逆比例する傾向にあることが知られている。この傾向は，発見者にちなんで「Pelgrom則」と呼ばれる。プロセス世代が進むと，素子面積は小さくなることから，Pelgrom則によりランダム・バラつきは大きくなる傾向がある。
ランダム・バラつきが発生する要因は大きく分けて２つあると言われている。（a）ライン・エッジ・ラフネス（line edge roughness：LER）と，（b）不純物密度の低下である。まず，（a）のLERを説明する。トランジスタのゲートは，指定されたゲート長とゲート幅を持つ長方形領域として形成されるはずである。ところが実際には，長方形の各辺は一直線には仕上がらず，凹凸を持つ。この凹凸がLERと呼ばれている。LERの影響で，トランジスタの平均的なゲート長やゲート幅は，目標寸法からのズレを持つ。LERは素子間で再現性がなく，ランダム・バラつきとして観測される。
次に，（b）の不純物密度の低下を説明する。微細化が進んできたため，トランジスタのゲート直下の不純物数が少なくなった。このため，不純物の存在位置によってSi内のフェルミ準位やエネルギー・バンド構造が変化した場合，トランジスタの素子特性に与える影響が無視できなくなってきた。不純物の存在位置に再現性はなく，この特性変化はランダム・バラつきとして観測される。
ランダム・バラつきは，素子間で無秩序に起こるため，複数の素子で構成される回路のバラつきは，単純に各素子のバラつきの和とはならない。例えば，平均遅延が100ps，ランダム・バラつきが10%（=10ps）の二つの素子で構成した回路を考える。この回路全体の平均遅延は，二つの素子の平均遅延の和である200ps（=100ps+100ps）になる。
一方，ランダム・バラつきは，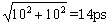
（平均遅延の7%）となり，二つの素子のバラつきの和（10+10=20ps）よりも小さい。このように，複数の素子からなる回路のランダム・バラつきは，素子数が多いほど減少する傾向となる。
距離依存バラつき
次の二つの傾向が同時に現れることがある。（i）ある素子がたまたま遅い仕上がりになると，隣接する素子も遅くなる傾向にあり，ある素子がたまたま速い仕上がりであれば，隣接する素子も速くなる傾向にある。（ii）ただしチップ上の同じ位置にレイアウトされた素子を，チップ間で比較しても無秩序にバラつく。
この二つの傾向が同時に起こるバラつきは，距離依存バラつき（狭義のシステマティック・バラつき）と呼ばれる。同一チップ上で素子間の距離に依存した相関があるためである。距離依存バラつきの発生要因は，光学装置の特性やウェーハの反りなど，一般に製造起因で発生すると言われている。
距離に依存して相関が変わるため，近距離に配置された素子で構成した回路では素子仕上がりの均一性が高まり，チップ間バラつきに似た傾向を示す。一方，遠距離に配置された素子で構成した回路では，素子仕上がりが無秩序に近づくことから，ランダム・バラつきに似た傾向を示すことになる。
スタンダード・セル内で一般に使われるトランジスタでは，距離依存バラつきは，ランダム・バラつきに比べて１ケタ以上も小さい。ただし，ランダム・バラつきは，素子数が増えると小さくなるという特徴があるため，回路構成によっては，距離依存バラつきがランダム・バラつきに対して無視できない場合がある。
デターミニスティック・バラつき
チップ上の特定の位置にレイアウトした素子が，どのチップを測定しても速い仕上がりになる。あるいは遅い仕上がりになる，と言うように，素子の位置を特定すると，バラつきが決まる場合がある。これをデターミニスティック・バラつきと呼んでいる。
デターミニスティック・バラつきは，主としてレイアウトに関係した要因で発生する。例えば，素子の粗密差による仕上がりの違い，ストレスによる素子の性能変化などである。既知の現象に対しては，現象をモデル化してタイミング検証に反映させる工夫や，レイアウトの均一性を増して，バラつきを減少させる工夫がなされている。
Derating係数で反映
一般的なタイミング検証方法であるSTA（静的タイミング解析）を使っても，OCVを考慮した設計や検証が可能である。以下では，その手法を説明する。
まず，あらかじめOCVによって遅い方向へバラついてしまった場合の遅延係数「α（late）」と，速い方向へバラついてしまった場合の遅延係数「β（early）」を用意する。そして検証対象の回路中で，遅い方向へバラつくとタイミングが厳しくなる素子には，その遅延値にα(late)を乗じる。一方，速い方向へバラつくとタイミングが厳しくなる素子には，その遅延値にβ(early)を乗じる。こうした条件で，STAを使ってタイミング検証を実施する。
この条件下でも，タイミングを満足するように設計すれば，OCVによって素子がバラついたとしても動作保証することができる。このタイミング検証で使用する係数をDerating係数，またはOCV係数と呼んでいる。
上述したように，Derating係数は，α（late）とβ（early）の2値からなる。また一般には，トランジスタと配線ではOCVがタイミングに与える影響が違うことから，ゲート遅延（素子遅延）と配線遅延に異なる係数を与えることが多い。
ただし，この検証方法では，係数に固定値を与えるため，ランダム・バラつきの特徴である「素子数が増加すれば係数が下がる」という現象や，距離依存バラつきの特徴である「距離によって，バラつき傾向が異なる」という現象を表すことができない。最近では，より正確なOCVの反映を目的として，Derating係数を素子数や距離に依存した値として定義できるSTAやSSTA（統計的STA）を活用する動きがある。
