公差を合成する
さて、ここからは公差を合成する方法について、説明しよう。機械部品では複数の部品の公差を統計的に合成する不完全互換性の方法(√計算)を使う場合、分散の加法性を適用する。電子部品でも、単純な足し算となる特性値に対しては、同様の方法が使える。
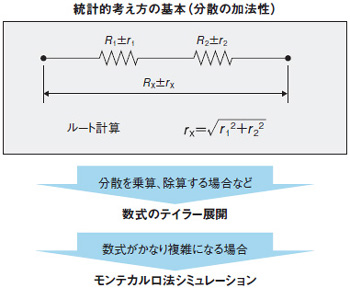
例えば、2つの抵抗R1(抵抗値がR1で、公差が±r1)とR2(抵抗値がR2で、公差が±r2)が直列に接続されている場合を考えてみる。この場合の合成抵抗RXは、
RX=R1+R2
で表せる。公差に関しては、分散の加法性を適用して、
rX=√r12+r22
となる。
これを応用して、先ほどのJIS C5063のE6系列の抵抗を使って、30Ωの抵抗をつくることを考えてみる。30Ωとするには、10Ωの抵抗を3つ使うか、15Ωの抵抗を2つ使うかだ。いずれも、合成抵抗は30Ωで違いはない。
さて、10Ωの抵抗を使った場合は、許容差20%(±2Ω)なので、3つを合成した公差は
√22+22+22=2√3
となる。一方、15±3Ωの抵抗を2つ使った場合は、
√32+32=3√2
となり、両者の値は異なってくる。同じ系列の部品を使っても、回路全体での公差計算結果が異なってくるのだ。
このように、直列に並んだ抵抗の公差を合成するのには分散の加法性が適用できるが、実際の電子回路ではさまざまな部品が複雑に関係する。特に、公差を単純に足し合わせるのではなく、乗算や除算が含まれる場合には、分散の加法性を適用できない。
そのような場合には、テイラー展開によって、公差分だけ変化したときの回路特性の値を導き出す。さらに、数式がかなり複雑になる場合にはモンテカルロ法シミュレーションを適用することになる(図1)。