《日経Robo》カーネル法は遅くない、乱択化フーリエ特徴関数で大規模でも適用可能に

本記事はロボットとAI技術の専門誌『日経Robotics』のデジタル版です

［画像のクリックで別ページへ］

著者の岡野原大輔氏

　機械学習の分野ではカーネル法と呼ばれる手法が広く使われている。1990年代後半から流行したSupport Vector Machine（SVM）は、このカーネル法を利用することで非線形な問題を扱えるということで注目された。

　カーネル法は、2つの要素x₁,x₂∈X間の"近さ"を定義したカーネル関数K（x₁,x₂）を利用する。カーネル関数は2つの値が似ているほど大きな値を取り、離れているほど小さい値を取るような関数である。

　例えば、ベクトル間の内積<x₁,x₂>はカーネル関数の1つである。よく使われるRBFカーネルはパラメータσ>0を伴って次のように定義される。

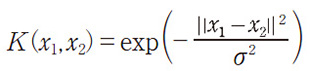
これは、x₁とx₂が全く同じ値であれば1、違う値（特に≫σ）の時、ほぼ0となるような関数である。

　自然言語処理などスパースなデータを扱う場合、多項式カーネル

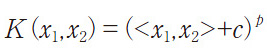
などが利用される。カーネル関数は何でもよいわけではなく、半正定値関数であることが求められる。次の条件を満たす場合に半正定値関数と呼ぶ。

「任意のn個の要素（x₁,x₂,…,x_n）に対し、K（x_i,x_j）=K（x_j,x_i）であり、かつ任意の実数a_i,a_jについて∑_i,_j a_ia_jK（x_i,x_j）≥0が成り立つ」

　カーネル関数が半正定値関数の時、

のように表せることが知られている（Mercer's theorem）。つまり、要素をある写像ϕで別の空間に飛ばした上で、そこで内積を取っているようにみることができる。なお、以降では対象の要素Xとして実数ベクトルR^pを考えるが、カーネル関数が定義さえできれば、文字列やグラフといった数値ではない要素も扱うことができる。

非線形問題を線形問題で扱えるようにする

　カーネル法の優れた点は非線形の問題を線形の問題の枠組みの中で扱える点である。これを説明するために、少し長くなるが、入力x∈R^pから出力y∈｛−1,1｝を推定する二値分類の問題を考えてみる。この二値分類の推定に線形識別器を使う。線形識別器のパラメータの重みベクトルをw∈R^p、バイアスをb∈Rとした時、線形識別器f（x;w,b）は

のように定義される。線形識別器は空間を、wを法線、切片がbであるような超平面で2つに分割し、与えられた点がその表側か、裏側かで二値分類していると考えられる。学習データ｛（x_i,y_i）｝に対し、それらをうまく当てられるかを示す損失関数l（x,y,f（x;w,b））を定義する。損失関数は学習データをうまく当てられている場合は0、当てられない場合は大きい値を返すような関数である。

　例えば、二値分類でよく使われるヒンジ損失関数は

と定義される。この損失関数の和を小さくするようなパラメータを求めることで学習を行う。さらに、パラメータの正則化として、重みベクトルのL2ノルム||w||²/2を加えた次の目的関数を考える。

このとき、損失関数が凸関数であれば、L2ノルムは凸関数であるため、それらの和であるLについても凸関数となる。凸関数は入力に対する勾配が0の時に最小値を取る。Lの重みベクトルwについての勾配が0になる条件を調べると、次のようになる。

ただし、l'（x_i,y_i,w,b）はlのwに対する勾配である。Lを最小化する最適なパラメータをw*、b*とし、α_i=−l'（x_i,y_i,w*,b*）とおくと、

となって、最適な重みベクトルw*は学習データの重み付き線形和として表せることが分かる。この表現を、最初の線形識別器の式に代入すると、

と表されて、線形識別器は与えられたデータと、学習データのそれぞれとの内積の重み付き和として定義できることが分かる。

　一般に、学習の目的関数がパラメータのL2ノルムを含み、かつ損失関数の中でパラメータwと入力xが内積<w,x>の形で出現する場合に、最適な重みベクトルはこのような内積の重み付き和として表現できる。ロジスティック回帰やAda Boostingなど広い学習器がこれに所属する。

RBFカーネルは複雑な分類曲面を形成

　ようやくカーネル法を説明する準備が整った。この最適な線形識別器の表現（ii）の内積部分<x_i,x>をカーネル関数K（x_i,x）に置き換えてみよう。

これは何をしていることになるか。前半で説明したように、カーネル関数は元の入力xを別の空間上の点ϕ（x）に変換し、その上で内積を取っているようにみなすことができる。つまり、内積の計算部分をカーネル関数に置き換えるだけで、あたかもϕ（x）の空間で線形識別問題を考えていることになる。元の空間では線形では分類できなかった問題もカーネル関数が定義する空間中では線形に分類可能にでき、その空間上で分類できる。

　例えば、RBFカーネルの場合、ϕ（x）は無限次元であり、その無限次元上で線形識別器を使っていることに対応する。それを元の空間でみれば、近いものはより近く、遠いものはより遠くにしたような歪んだ空間に対応する。

　カーネルが対応する空間での超平面は元の空間では非常に複雑な分類曲面に対応する。また、カーネル関数の計算は高次元に展開して内積を明示的に求めるよりもずっと高速に求めることができる。RBFカーネルは無限次元間の内積であるにもかかわらず、その値はベクトル間の四則演算とexpの計算だけで求められる。これを、カーネルトリックと呼ぶ。

遅かったカーネル法を一変させたRFF

　カーネル法は強力であり、SVMをはじめとしたカーネル法は一時期、機械学習の世界を席巻した。一方で、当時のカーネル法は計算量が大きいという致命的な問題を抱えていた。例えば、学習事例数がNの時、カーネル法を使った手法の学習時の計算量はO（N³）（オンライン学習やスパース化など工夫をしてもO（N²））であり、その利用時の計算量も（iii）の式からわかる通りO（N）時間かかりる。

　機械学習は学習事例が多いほど強力であり、現在はN=10⁶～10⁹が使える時代であるから、カーネル法の計算量は大きな問題となり、「カーネル法は精度が良いが遅く、大規模データには使えない」とこれまで認知されていた。

　こうした状況を変えたのが2007年に登場した乱択化フーリエ特徴関数（RFF: Random Fourier Features）を使ったカーネル法の高速化手法である^1）。RFFはカーネル関数がK（x₁,x₂）=ϕ（x₁−x₂）のように、差で表現される場合に使える方法で、先ほどのRBFカーネルなどがそれに当たる。そのフーリエ変換は、次のように表せることが知られている。

ここで、p（ω）はRBFカーネルの場合は、それぞれの成分が正規分布N（0,s²）に従うことが分かっている。この積分値をp（ω）に従ってωをm個サンプリングし、モンテカルロ近似する。

ただし、

である。ここでは、cos（α−β）=cos（α）cos（β）+sin（α）sin（β）を使った。つまり、カーネル関数はランダムに選んだフーリエ特徴の内積で近似できる。

　このサンプリング数mは大きくなくてもカーネル値の近似が精度よくできることが分かっている^2）。特徴ベクトルを陽に表せられるため、このRFFを使ったモデルは従来の線形モデルと同様の計算コストですみ、データ数Nに対してO（N）の計算量で学習し、O（1）時間で関数評価をすることが可能である。

ニューラルネットでカーネル関数を学習する研究も

　この変換が何をしているかの直感的な説明をしよう。ωは周波数に対応しており、x₁とx₂が近い値であればωが大きい値（高周波数）になったとしても、ωx_i（i=1,2）の値は近い値をとり、結果として対応する特徴値の符号は同期し、それらの積は正の値を取る。一方でx₁とx₂が違う場合、周波数が大きくなると、ωx_iの値は大きく異なる。その特徴値の正負はほぼランダムになり、期待値は0となる。結果として、x₁とx₂が近い値であれば1に近い値となり、そこから外れると急速に0に近づく。

　さらに、この乱択化特徴量の計算を高速にするために、それぞれの特徴値を独立に計算するのではなく、構造化された計算を使うことで、元の特徴次元数が多くても高速に計算できる手法も登場している^3）。他のカーネル関数でも同じようなアイディアが適用できるか、またカーネル関数のパラメータについての勾配も計算することでニューラルネットワークと組み合わせてカーネル関数自体を学習するような研究も始まっている。

　こうした改善から、カーネル法は今やデータ数に対して線形の計算量で求めることができ、大規模なデータにも適用できるようになった。

岡野原 大輔（おかのはら・だいすけ）
Preferred Networks 取締役副社長

2006年にPreferred Infrastructureを共同創業。2010年、東京大学大学院博士課程修了。博士（情報理工学）。未踏ソフト創造事業スーパークリエータ認定。東京大学総長賞。