公差設計をしていく上で身に付けておくべき知識は幅広い。ここでは，中でも基本的な知識について解説していきたい。公差を勉強し始めたばかりの技術者だけでなく，公差の基本知識は十分に持っていると自負している技術者も，あらためて読んでみてほしい。当たり前だと思っていたことでも，実はある一面しかとらえていなかったケースがあるかもしれない。

緩めても安くならない？

公差を厳しくすれば製造コストが高まり，公差を緩めれば低くなる─。公差を考えるときの基本はその通りだが，実は逆の場合もある。工程能力に余裕があるなら，公差を変えてもコストは変わらないこともある。

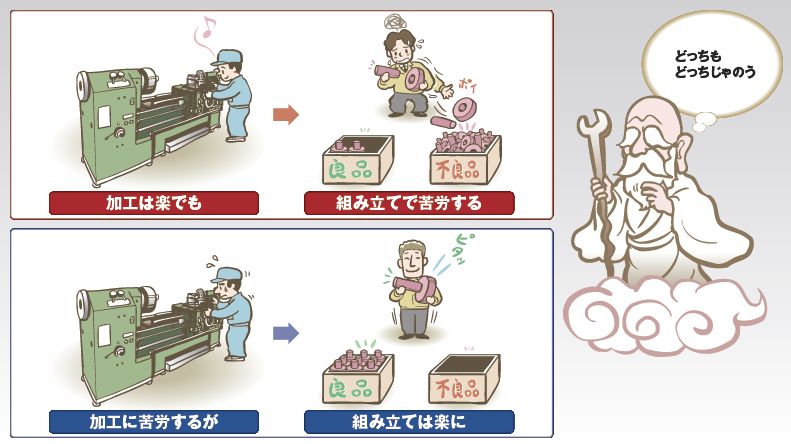
例えば，公差が緩すぎると加工は楽になるが，後工程でトラブルが発生しやすい（図1の上）。組立工程に投入する前の部品を測定してランク分けする必要が生じたり，作業者が現場でトライ・アンド・エラーでぴったりはまる部品の組み合わせを探ったりする事態を招き，思わぬコストが発生するのだ。

逆に，公差を厳しくすると加工コストは高まるが，そのように生産された高精度の部品は後工程での組み付け不良などを起こしにくい（図1の下）。バラつきが小さいので，組み立てやすいのである。

公差の厳しさとその影響
公差を緩めると加工は楽になるが，後工程の組み立て時にトラブルが発生する可能性が高まる。逆に，公差を厳しくしすぎると組立工程でのトラブルは抑制できるが，加工で苦労することになる。生産プロセス全体を見ながら，部品ごとに最適な公差を設定することが重要だ。

特に，設計の分業化が進んで技術者一人が担当する範囲は狭まっている場合は，とかく全体的な視点が欠けがちだ。モジュール単位で公差検討することを否定するわけではないが，最終的に製品として完成するまでの工程を俯瞰しながら，公差検討することが大切なのである。

最悪ケースだけを考えない

公差を設定した個々の部品を組み立てた場合に，アセンブリの公差がどのようになるのかを計算する方法には，大きく二つの考え方がある。一つは，各部品の公差を単純に合計する「互換性の方法」，もう一つが統計的に処理する「不完全互換性の方法」と呼ばれる考え方だ（図2）。

公差の集積
部品のバラつきが公差範囲内の両極端になった場合を考える「互換性の方法（Σ計算）」と，統計処理によって計算する「不完全互換性の方法（√計算）」がある。

互換性の方法では，各部品の寸法が公差域内で両極端になったケースを考え，それをもってアセンブリがバラつく範囲とする。単純に五つの部品（公差が±a，±b，±c，±d，±eの5部品）を積み上げていく例で説明しよう。この場合，すべての部品の寸法が最も大きくなる値（公差の＋側）の積算と，すべての部品が最も小さくなる値（公差の－側）の積算である。つまり，アセンブリの公差±Xは，

X＝a＋b＋c＋d＋e

となる。このように単純に加算していくため，互換性の方法は「Σ計算」と呼ばれることがある。

一方の不完全互換性の方法では，各部品が正規分布でバラついていると考え，「分散の加法性」＊を利用してアセンブリの公差を計算する。製造する部品の数が十分に多い場合には，すべての部品が最悪ケースとなる確率は非常に低くなるという考え方だ。

具体的には，上記と同様の5部品を積み上げることを考えた場合，アセンブリの公差±Xは，

X＝√a2＋b2＋c2＋d2＋e2

となる。このような計算式となるため，不完全互換性の方法は「√計算」とも呼ばれる。

基本的に，互換性の方法で計算したアセンブリの公差値の方が，不完全互換性の方法で計算した公差値より大きくなる。逆に，あるアセンブリの公差を実現するために，各部品の公差をどのようにすればよいのかを計算した場合，不完全互換性の方法では公差を比較的緩く設定できる。つまり，加工コストを低く抑えられるわけだ。

ただし，不完全互換性の方法では各部品が公差を満たしていたとしても不良品がある確率では発生することになる。この確率は，ある程度の生産数があってこそ事前に予測できる数字。生産数が少ない場合には予測しづらくなるので注意が必要だ。

実際の公差設計においては，Σ計算と√計算だけでなく，「これらを組み合わせた独自の計算式を使う企業も少なくない」（プラーナー代表取締役の栗山弘氏）。Σ計算では厳しすぎ，√計算では緩すぎるといった場合に，適切な評価が可能なように各社が考え出したノウハウ的な式である。